ラプラス変換の微分積分・一次遅れやインパルス応答・インディシャル応答の式の説明が分かりやすい本

そういった式やグラフのイメージがわかりやすい本の１つが、

「スバラシク実力がつくと評判のラプラス変換キャンパス・ゼミ―大学の数学がこんなに分かる!単位なんて楽に取れる!」

でした↓

著者は、馬場敬之（ばばけいし）さん。マセマ出版。（アマゾンレビューみたら、マセマ出版って、この分野では有名な出版社なんですね）

私自身は組込みシステムのエンジニアとして仕事で必要なので読みました。最近、機械制御の業務をすることになって、必要になったので勉強を始めました。

業務で、ブロック線図が出てきて、その中にラプラス変換の式が出てきます。

ラプラス変換で表す式の意味やイメージが分からないと仕事ができないので本を読み漁ってきました。

その中の一つが、上記で紹介した本。

業務で、組み込みシステム・電子系の現場エンジニアにとって、

本書で直接役に立つのは、本書の最後の方のappendixの章「自動制御入門」でしょう。

※３０日間無料体験のAmazonキンドルに加入すれば、その期間にキンドル本については無料で書籍が読めてしまいます。

ラプラス変換の微分積分・一次遅れやインパルス応答・インディシャル応答の式

一番重要で、必要な時に取り出したい情報を書きにメモ書きしておきました↓

213ページのラプラス変換の一覧

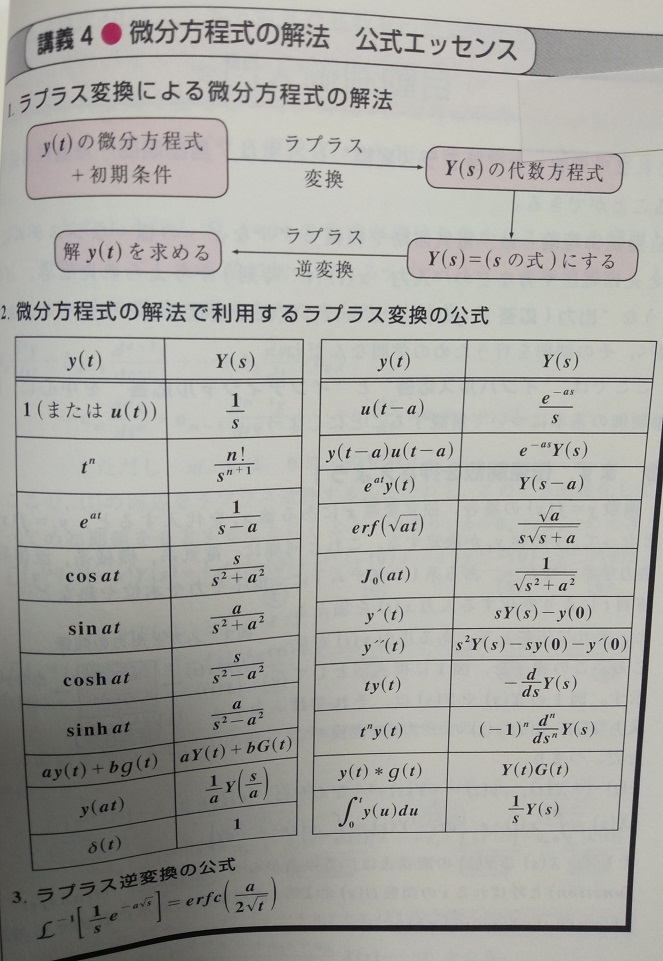
その後のページに書いてある、

伝達関数の基本形。

比例要素、微分要素、積分要素。

そして1次遅れ要素↓

こちらの完成形の式。

そして、218ページと219ページに書いてあるインパルス応答とインディシャル応答。

パルスの入力と、それに対する出力のグラフのイメージ。

ブロック線図を読んだり、電子回路の応答をイメージするために役に立つ内容です。

現場のエンジニアが実務で使う人は、本書のappendix を読むのが一番役に立ちます。

ちなみに、本書の一番の対象読者は、

大学で理工系の数学を学んでいる人でしょう。

アマゾンのレビューを見ると、

「大学院院試で役に立ちました」

と書いてあるコメントがいくつかありました。

理工系の大学で、大学院に行くための試験に役に立つ本なのでしょう。

ラプラス変換、ラプラス逆変換、微分方程式について、

例題が豊富にあります。

式の解き方、どうやって式を変形していけるのか？

について詳しく書いてあります。

私は現場の実務で使うために読んだので、正直、本書の前半と中盤の式の変形のところはパラパラっとめくっただけでまともに読んでいません。

というより、読んでも意味が分かりません！（苦笑）

こんなふうに式を解くんだなーくらいの感覚です。

「スバラシク実力がつくと評判のラプラス変換キャンパスゼミ　大学の数学がこんなにわかる単位なんて楽に取れる」

というのは、本のタイトル通り大学で数学を学ぶ人がメインの読者です。

現場の業務で使う人にとっては、本書後半の完成形の式やグラフのイメージ図のところが役に立つでしょう。

（現場の組込みシステムのエンジニアではなく、企業で研究所のようなところで仕事をされている方は、本書の内容がまるまる役に立つのかもしれません）

※３０日間無料体験のAmazonキンドルに加入すれば、その期間にキンドル本については無料で書籍が読めてしまいます。